第4回の授業の幹

遠隔授業2020		＜従来の何回目に対応するか＞
第1回　9月17日	算数の学年配当A・B領域	低学年の加減・補助記号，発達段階
第2回　9月24日	算数の学年配当　その他の領域	量の4段階指導　＜第6回＞
第3回　10月1日	四角形のカタログ	長方形の定義，対称，＜第2回＞
第4回　10月8日	敷石探検隊	＜第3回＞
第5回　10月15日	パノラマ	＜第4回＞
第6回　10月22日	30度のお湯を足すこと	＜第5回＞
第7回　10月29日	53を503と書く	＜第1回＞＜第7回＞
第8回　11月12日	電卓を使って	＜第8回＞＜第9回＞
第9回　11月26日	掛け算・割り算の筆算，小数・分数	＜第9回＞
第10回　12月3日	タコの掛け算七七	＜第10回＞
第11回　12月10日◎	算数の習熟とゲーム	＜第11回＞＜第12回＞
第12回　12月17日	教科書の著者の意図を読む（特に折れ線グラフに注目して）	＜第13回＞
第13回　1月14日	教科書の著者の意図を読む（特に低学年に注目して）	＜第14回＞
第14回　1月21日	作品の相互評価	＜第15回＞

　第4回の授業の，　まくら。

　落語には，「まくら」という言葉があります。寄席と学校と，どちらもしゃべる仕事ですが，学校では，「はい，チャイムがなったら，すぐに席に戻って，授業の準備をするんだったよね」などと，先生が偉そうに指示をしますが，寄席では，聞き手はお客様ですので，そんな，あからさまな指示ができるはずはない。そこで，

「え〜（と大きな声で，お客がおしゃべりをやめて，こっちを向くように仕向ける）。こんちまた，大勢のお客様のお運びで，ありがとうございます（と，礼を言っておくのが無難）。夏ともなりますと，怪談話がもてはやされるようで，…（と，時候の挨拶と見せかけて，本日の演目へのお客の興味を持たせるようにだんだん…）」

と本題に持って行こうてのが，まくら。興味をつなげるだけではなく，古典落語だと，昔の話だから，昔のことがわからない。特にそれが最後のオチに関連することだと，せっかくのオチがわからないから，話が台無しになってしまう。そこで，さりげなく，「昔は，道具屋という商売がありましてな。ちょうど，ブックオフさんが，本でやっているように，お客から中古品を買い取って，他のお客に売る商売のことです。≪古道具屋≫と言ってたのの，最初の≪古≫がとれたんですね。」と説明を入れておく。学校の先生とは違って，教えてやるぞではなく，さりげなさが肝心。言葉だけではなく，三味線の細棹と太棹との違いとかを，まくらで説明したりもする。

　今回は，皆さんにパズルをしてもらいます。本当は，まくら　を振りたいところですが，こんちのお客さんは，すでにお手元にパズルの材料がありますからね。やってみたくてしょうがなくて，まくら　を聴いてはくれなさそうです。そこで，まくら　を授業の途中でという変則的な進行になりますが，どうかお許しを。

　レターパックに，いろいろなものを詰め込みましたが，第4回は，

紙を開くとこんな感じ。

（C）透明シートと，スナップボタンが，はさまれている束 束の中に，いろいろ。 ・ 第4回　10月8日 敷石探検隊　で，行うパズルの台紙。 ・ 第5回　10月15日 パノラマ　で使うワークシート。 ・ 同じく，第5回で使う，「秘密兵器」だけど，あらかじめ第0回として，レターパックが届いたら，作っておいて欲しい。（その第0回の説明は，このファイルの後半に資料として載せます。） ・ 第4回　10月8日 敷石探検隊　を普段の年度の対面授業で行う際の授業プリント。 ・ 第4回のパズルで使う，各問での5つのピースを作るための色画用紙

ですよ。「パズルの台紙」，「第4回のパズルで使う，各問での5つのピースを作るための色画用紙」，

それと，画用紙を切るためのハサミ（誰です，洗濯ばさみを持ってきたのは！），そしてノリ（スティックのりがよろしいようで。おにぎりを作るあれではございません。）も用意しましょう。それと，「敷石探検隊　を普段の年度の対面授業で行う際の授業プリント。」は，あとの授業途中の≪まくら≫で使います。

　いろいろとプリントが多いですから，「もう使ったもの」は，レターパックの外側に出して，ファイルなどで整理しておくと，実際の先生になったときの参考になりますね。そして，「まだ使ってない」のは，レターパックの中に。あ，そうそう。『初等教育論集』は，4年生の時に卒業研究報告書を書く際の参考に。4年分ためておくのがよろしいのです。それと，『すくすく』は，今度はご自分が書く番になったときのために。この2冊は，書棚に入れておきましょう。

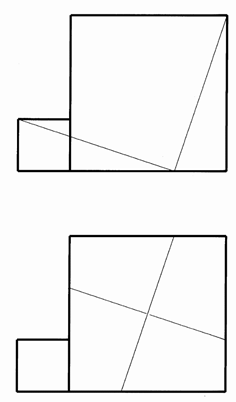
　さて，パズルです。問1・問2とがあります。切り離して，問1なのか、問2なのか入り混じると困るので，色が違えてあります。でも，どちらも，大小2つの正方形に細い線が引いてありますね。２つの正方形を細い線で切り離すと，どちらも5つのピースになります。さて，この5つのピースを重ねずに，5つ全部のピースをぴったりつけて，１つのさらに大きな正方形を作りましょう。

2つの正方形　　→　5つのピース　　→　１つの正方形

念のため言いますが，作るのは，正方形ですよ。「先生できた」とお澄まししている人のを見せてもらうと，できた「正方形」の辺の長さが，元のおおきな正方形の辺の長さに等しくなっている人が時々います。

[大きな正方形の面積］＋[小さな正方形の面積］→［できあがりの正方形の面積］

ですから，できあがりの正方形は，最初の「大きな正方形」よりも，ちょっと辺の長さが長くなるはずで，同じってことはないですよ。

　人によって，得意不得意がありますから，問1よりも前に問2にチェレンジしても結構です。この２つのパズルを，ハサミで切り離すところを含めて，制限時間２つのパズル合計で8分でやってみましょう。

　そして切り離したあとで，最初はどうだったのか，知りたい人のために，「台紙」があるのですね

＜8分は，ご自分で測って下さい。はい，いいですか？　よ〜い…，ドンッ＞

8分経ったぞってことを，知らせるのに，普通の授業では，

「敷石探検隊　を普段の年度の対面授業で行う際の授業プリント。」

を配り始めるようにしています。こんな感じで，プリントを配るタイミングって，授業の時の流れのアクセントに使えることがありますね。

　では，このプリントを眺めてから，次の説明に進んでください。「おあとが，よろしいようで」。

　さて，「○○の形は，××だ，それは…」で始まるエッセイを，文系数学（基礎）の最初に書いてもらいましたよね。「タイルは正方形である」ってのはどうですか。

　平面を敷き詰めることができるので，お風呂場などに敷くのに，水漏れがしないようにできるから，正方形が都合いいのですよね。でも，平面を敷き詰めることができる，正多角形は，四角形だけではないですよね。ここら辺を，詳しく証明も含めて扱いたいところですけど，ま，必要な人は，ググッたり，ヤホったりしてもらうことにして，答えだけ言うと，３，４，６ですね。そして，6は向かい合う頂点を対角線で結ぶと，6Pチーズみたいに切ることができて，3角形の敷き詰めになっちゃうだよね。

　では，「正四角形で，平面を敷き詰めることができる」ってことを，いま，　四　を疑ったけど今度は，正　を疑がってみよう。

　アメリカでは，What if not ってことばがあります。「そうでなかったらどうなるの？」みたいな感じの言葉です。単に計算させたり，覚えたりするだけではなくて，数学を勉強するからには，新しい発見ができるような，将来の数学者っぽい人を育てる教育が必要だという文脈から，この言葉は珍重されたわけです。

　で，正方形でなかったら，どうなるの？　ですね。普通の年度で，対面授業で一斉にするときには，平行四辺形のタイルを大量生産したとして，それで平面を「〇：敷き詰められる」と思うか，「×：敷き詰められない」と思うか，手を挙げさせて，人数を数えて，それから，ちょっともったいぶって，種明かしをしていきます。ええ，どうぞ，下に書いておいてください（本当は人数を書きたいのですが，ご自分だけだから，1と，どっちかに書くことになります）。

じゃあついでに、アンケートのところに書いておいてください。なお、凹四角形とは「ブーメラン型」のことです。

ちなみに，敷き詰めるってのは，辺が隣のタイルとぴったりついていて，頂点のまわりのぴったりしていること。でも，平面というのは，無限に広がっているので，部屋の端では，どうするのってことは，気にしない。ま，実用的には，絨毯と同じで，部屋の端で切ってサイズを合わせることはOKです。

　こんな目の付け方で，街を歩くと，面白いタイルの敷き方に出会えますよ。

　さて，お次は，「1種類の正四角形で，平面を敷き詰める」の，「1種類の」のところを，疑ってみましょう。2種類の正方形のタイルの敷き方は，いろいろとあるのだけど，それぞれの枚数が同じ枚数になる敷き方って…。

　ちょっと端折りましたが，だいたいここまでが，パズルの答えへの「まくら」です。 index.htm