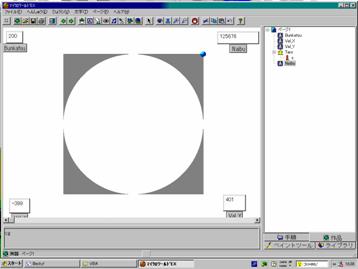
円周率を円の面積で求める index.htm
原点を中心に辺の長さが2の正方形を考えます。2という数は,中心から外周までの距離が1にするためです。つまり半径1の円に外接する正方形ですね。その縦横を何等分かして,小さな正方形に分けます。その小さな正方形の中心が円の内部か,外部かを,原点からの距離が1以上かどうかで決めます。
円周がその小さな正方形に含まれているときには,その面積は0でも,小さな正方形全部ではないので,内部か外部かとは言えないのです。そこで,ここが誤差の原因になってしまいます。この誤差が生ずる部分は,上端,あるいは右端に集めることができますから,誤差は,輪郭の正方形の半周に,小さな正方形1辺の長さの厚みを掛けたものを上回らないはずです。
円の面積は,
(小さな正方形の面積)×(円の内部として判定された小さな正方形の個数)
で,求めることができます。また,円の面積は,
(半径)×(半径)×(円周率)
で,この場合の半径は1ですから,実は円の面積の真の値は,円周率です。分割数を大きくすればするほど,円周率の正確な値を求めることができるという訳です。
分割数を200にするときれいな円がかけますが,かなり時間が掛かります。いまの私の自宅パソコンでは,1時間以上掛かりそうですから,授業で実行するわけにはいきません。せいぜい100程度かもしれません。プロジェクタで初めのところを映して,シャッターを閉じて,その間に授業をして,最後に計算結果をみる。でも,その間生徒は気になって気になって。授業どころではないでしょうネ。
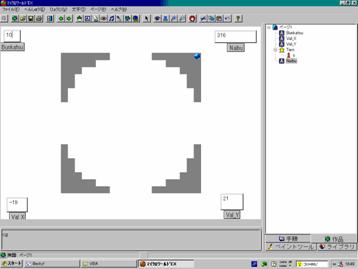
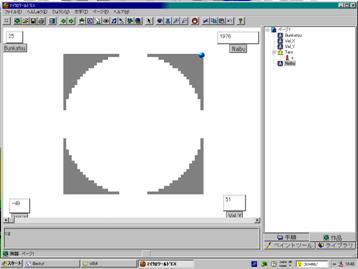
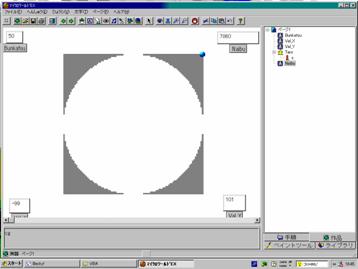
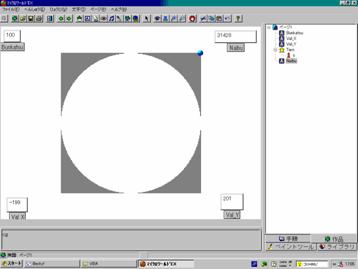
だから,分割数10とか20程度でやってみて,後は結果だけ示すってのが,よろしいのではないでしょうか。その結果だけ示すために,実行結果を貼り付けておきましょう。
|
分割数10 : |
|
分割数25 : |
|
分割数50 : |
|
分割数100 : |
|
分割数200 : |
文書の先頭 index.htm プログラムのリンク:rudolf.mwx
プログラムは,MicroWorld によったもので,残念ながらこれがインストールされてない機械で見るには,この製品か,http://microworlds.jp/ の「ダウンロード」で無料で提供されている,WebPlayer をインストールする必要があります。なお,MS Excelのマクロでやってみようとしましたが,作業の途中を絵で示すことはしないで,最終結果を一度に表示するので,こうした見せ方にはなじまないと判断しました。