../index.htm （もどる）
小笠教育研究協会数学教育研究部 一斉研究報告会（中学校部）
|
平成２９年１１月８日（水） 静岡県菊川市立菊川西中学校 |
の授業に関する、研究協議（14:30〜16:30）の後半（50分くらいの目安）での話題提供のレジュメ。
正 田 良（rio@kokushikan.ac.jp）
１）単元は、「相似」ですが、その後半部分であって、「平行線と線分の比についての性質」を
「三角形の辺が、直線によって分けられる比を求める」へ応用する場面が、本時の授業として
予定されています。
２）この部分は、学習参考書風に言えば「平行線は線分の比を移す」と言語化（まとめ）して、
それを手掛かりとする問題解決が行なわれます。補助線をうまく引くと良いとされていますが、
どう引くのか。
・ 比が既知の（同一直線上の）線分の組は何か。
・ 平行な直線は引かれているか。引きやすいか。引いて有用そうか。
３）また、こうした数学世界に乗っかった問題解決の他に、（授業で扱うべきかどうかは、ここ
では度外視します）そもそも人類が、そしてその一員である生徒が、どのような経緯で、あるいは
どのような理由で、線分の比なることを考えた（考えないとならない）のか。
すこし、本日の授業とは文脈が異なっているであろう話題提供もします（恐らく、時間配分と
しては、大きな割合を占めるかもしれません）。
４）GeoGeblaを用いて、「やるべき課題をしっかりと把握し，それに向かって意欲的に学習に取り
組ませる」という試み。GeoGeblaをいち早く取り入れられている先進的なご研究との関心をもっ
て、当日楽しみにさせて戴きます。
私は不器用なもので、新しいものに慣れるのに時間が掛かってしまいます。GeoGeblaを当日ま
でにマスターできないと思いますので、３）のプレゼンは、Logo処理系のひとつMicroWorld
（ http://www.microworlds.jp/index.html ）によるものです。
正田のHP http://kks-el01.sakura.ne.jp/ar09/bucho/mwex_tip/index.htm
で、そのファイル TurtleBalance.mwx を公開しますが、残念ながらMicroWorld EXがインス
トールされているか、WEB Player を使うかでないと、見ることができません。
ただ、このLogoのカメさんは、パイソンとか他のプログラミング言語の描画機能に採りいれら
れています。（パパートなどの「ラディカルな開発主義」という学習理論で有名）
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
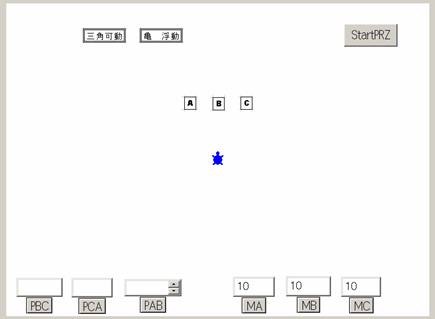
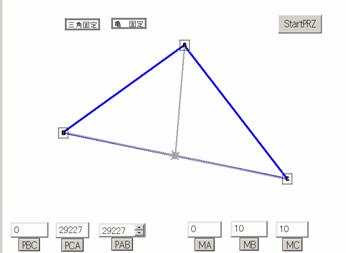
【図１】初期画面です。右上の、
を押す（クリックする）ことで、この状態へ戻れます。
は３匹の着ぐるみを着たカメさんですが、頂点の役割を演じさせています。お好きな位置
にマウスで引っ張っていってください。三角形の形が決まったら、
を押してください。青カメさん
が三角形ABCを描いて、ここの表示が、
に変わります。
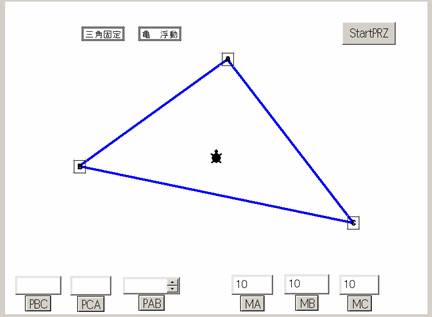
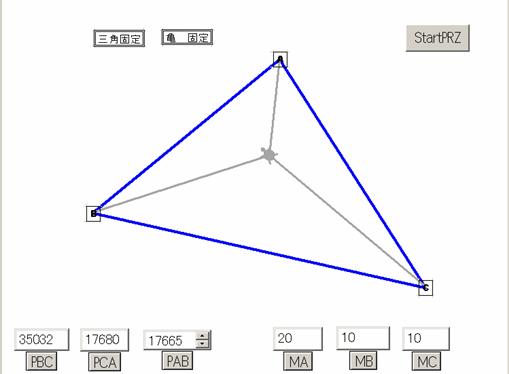
【図２】この三角形の頂点に おもり を下げましょう。
Aに付ける おもり の重さを、MAの欄に
Bに付ける おもり の重さを、MBの欄に
Cに付ける おもり の重さを、MCの欄に
書き入れてから、
を押してみてください。
になりました。
【図３】釣り合いの位置を、カメさんが教えてくれています。
左下は、カメさんが計算した三角形の面積です。釣り合いの位置をPとして、三角形の名前が表示されて
います。面積の公式を
を使ってプログラムしましたが、残念ながら有効数字３桁さえも怪しい。。
そのご愛嬌の誤差と割り切って、飽くまでも、予想推測の補助と思って下さい。
さて、線分の内分点・外分点って、なぜ人類が考えたのか。恐らく、棒に付けた２つのおもりの釣り合いを
考えたのでしょう。
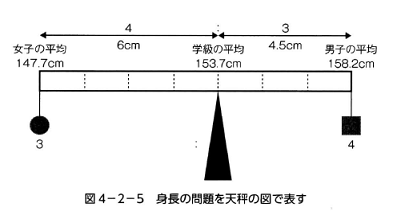
【図４】１次元の釣り合いは、線分の長さの逆比として
（おもりのおもさの、加重平均）
出典：正田 良，2014『濃さの向こうに広がる世界』学校図書。ｐ.107
MAを0にすると、Bに付けたおもりとCに付けたおもりの釣り合いの位置を調べることができます。
再度
を押すと、【図２】の状態に戻れます。
|
|
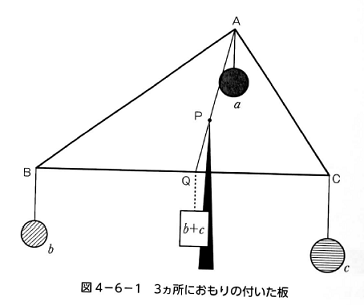
線分は、一次元単体。三角形は二次元単体です。二次元での釣り合い…。
|
【図６】２次元での釣り合い （前掲 （正田，2014）の p.123） |
そんなことを考えるのって、面白くないですか？
△PBCの面積と、△ABCの面積の比は、底辺が共通ですから高さの比です。それは、図６で
いうPQとAQとの比ということになります。線分AQという１次元の棒で釣り合いを考えると
AP：PQ＝（b + c）: a という、頂点に付けられたおもりの重さの比で表せます。つまり，
△ABC：△PBC＝（a + b
+ c）: a なのです。△PCA，△PABでも同じように三角形全体
△ABCとの面積の比を考えると、
おもりの重さの比は、
釣り合いの位置と対辺とで決定される三角形の面積の比に一致する。
残念ながら、私の独創ではなく、ニュースソースがあります。
1）バルク『重心の概念の幾何学への応用』東京図書・数学新書
前掲（正田，2014）に、ちょっとだけですが紹介しています。
ロシアが、ソビエト連邦と言っていたころ、純粋数学の研究者は、社会への貢献として青少年の
ための数学読み物を書くという義務があったそうです。そうして書かれたものが、上記の「数学新書」
シリーズとして日本でも翻訳されていました。
2）黒田俊郎先生の、教育実践。 雑誌『数学セミナー』や、三省堂のバイパスシリーズ。
特に、『平面幾何のは・な・し』（1999）。 なんでこうした概念を考えないとならないのという生徒の
疑問に、真摯に向き合って応えた高校の数学の先生としての豊富な経験。
正田（編著），『算数・数学って怖くない』成文堂，2011増補版
にも、塩の実験による内心などの執筆をお願いして、収録できました。
（実は，このいまでは入手困難な２冊の紹介をしたいというのが、前掲の（正田，2014）を
書いた動機のうちのひとつなのでした。）
今回の授業で扱われた三角形に、ちなんで、カメさんを動かすと、
|
【図７】Aのおもりと，Bのおもりの比は，2：1だから… |
BとCのおもりを、１か所にまとめると、場所はBCの中点、重さは20。これと、Aについて
いる おもさ20のおもりとの釣り合いの場所にカメがいます。
さて、問題解決の過程を分析しておきましょう。今回、学習指導案の９月15日版では、
|
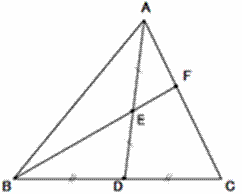
BCの中点をD，ADの中点をEとするとき， AF：FCを求めよう。 【図８】9/15指導案での問題 |
|
が主発問となっています。
そして、問題解決のためのツールは、ちょっと前の時間になりますが（問題の「見通し」が必要か）。
「平行線は線分の比を移す」
でありそうです。
・移す先は？
・線分の長さの比が既知であるのは？
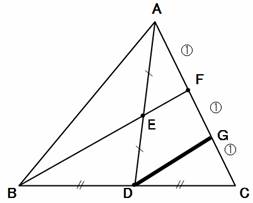
そうしてみると、図９の補助線は、自然な考えです。△ADGを書いてしまえば、比を移す必要から、
逆さの三角であるCFBに気付けるという趣向。
|
【図９】第１の補助線 |
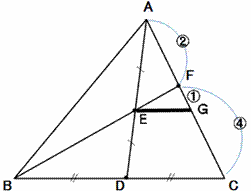
【図10】第２の補助線 |
図10は水平な直線であるという点では、思考として安定感があります。ただ、図10のEGの長さを、
CDを介してさらにBCとの比を考えることは、すべて「底辺での比」の話となるので、やや難しい。
しかし、別証をいろいろ考えてみようという発想があれば、知的な面白味がありそうです。
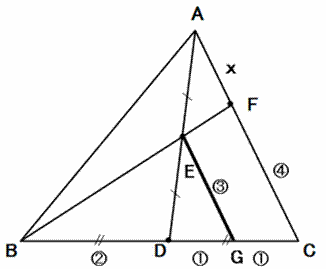
【図11】第３の補助線
点を通り、どれに平行という補助線ですから、この場合有限で、図11のような第３のものも考えら
れる。また、Dを通ってCAに平行な直線を引く第４のものもありですよね。こうした別証の発展的な
とらえ方を秘めた教材。ただ、こうした思考に生徒をいざなうための言葉掛けは、練っておかないと、
生徒の思考は、こちらが思うようには動きにくい。
また、途中の点を線分の比を変えることで変化させてみる。動的なとらえ方もこの学習指導案に示さ
れているので、当日楽しみになります。ただ、Dを動かすより、Eを動かす方が、工作としては自然
かなって気がします。
EがDからAに向かって、 1/3のところ、1/2（この問題）のところ、2/3のところ …など、表を
書いて変化を見るのも面白そうですし、それがGeoGebla で実現できるってのも、あり得ますね。
ただ、限られた時間での授業ですから、あまり余分な要素を付け加えてしまうと時間が足りなくなり
そう。そんな心配もします。もっとも、これから皆さんでの検討が為されて本番を迎えられるとのこと
ですから、それは杞憂でしょうけど。
以上、レジュメと言うより、当日の研究授業を楽しみにしますとの
メッセージとしてお届けします。 （2017.10.09.）
../index.htm （もどる）